English translation of Réseau vivant
Excited after having read the special edition of Pour la Science (french edition of Scientific American) about Alan Turing, one of the founding fathers of computer science, I scribbled on the pages some schemas about organization of computer network. Also with inspiration from works of Edgar Morin about complexity of living organism and its self-eco-organization, I asked myself if, instead of an organization from outside, computers can, like a living organism, self-eco-organize.
This means that computers can organize themselves in a network with consideration of environment, without that an external agent intervenes. After some shilly-shallying, here is the fruit of a logical-trigonometrical-boogie-woogie-computer science reflection.
Self-eco-organized network
In order to make computers forming a viable network, there are needs for each one of them to know, at least, where it is in the network and for others to find it in the network. Thus, each one should have an address, which is the reason why they have an IP (Internet Protocol) address defined from outside by people who created the network. But can the computers self-eco-organize thems after tools and specific knowledge have been implemented ?
Here are steps for a possible self-eco-organization of a computer grouping:
1a) A circle defined by its centre and its radius, considered as an entity. We suppose this entity has concepts of dot, line and angle.

1b) This entity is either created by the outside environment with the divine will or it is self-eco-created by elements from the milieu. So, we suppose that in the beginning there is something, but here it isn’t the question.
2) We suppose also that this entity has capacities to create straight lines going through its center and, perpendicularly, by his circumference.
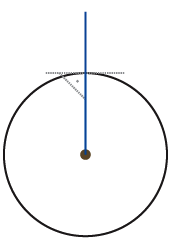
3) This entity also knows how to recognize a fellow entity and to exchange informations with the other (to communicate).

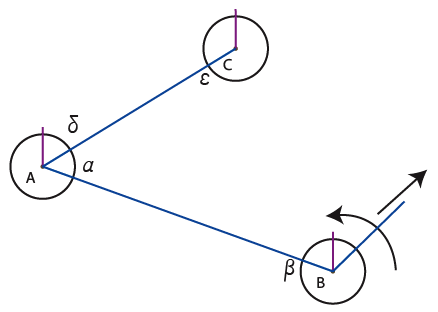
4) A first entity (A) establishes a first straight line immutable of reference (axis). This allows it to distinguish different directions by angle ratio.
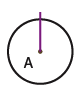
5) A second entity (B) arrives and creates a random line (communication channel). This channel meets at a time or another, after elongation and rotation, its congener (A). The last one accepts the channel and, when the channel is inside the circle, gives instructions to (B) to adapt itself to A’s own center.
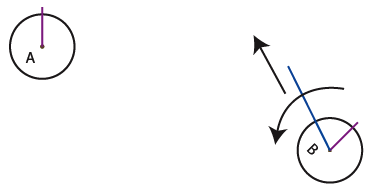
6) To situate one another, the relationship between the channel and the referential axis must be complementary. Under this circumstance, the sum of angles is 180°. By protocol, the new incoming entity adapts itself according to its partner. As a result, (B) turns around its own axis without the connecting channel follows it, and it stops once the angle β between its axis and its channel correspond to 180° minus the angle α communicated by (A).

7) This way, the entity (A) gets the address of angle α for entity (B) and this one has the address angle β for (A).

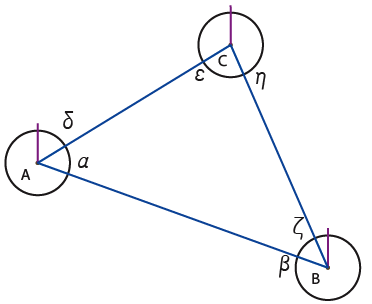
8) Then comes the entity (C) who is searching to be connected to a congener.
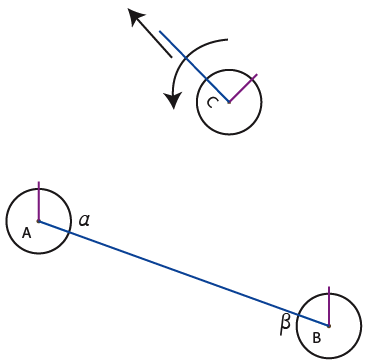
9) The third associate connects itself to (A). The one who has the most of connections decides its own address and the address of the new comer.
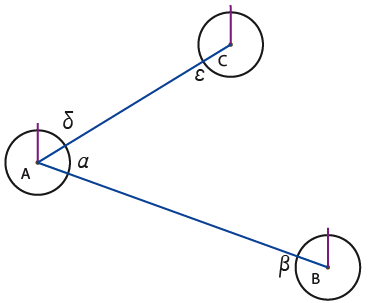
10) An existing entity is looking for a connection.
11) The entity who is looking for a connection connects itself and, in case of equal connections per entity, they decide mutually which addresses they give to each other depending on addresses they both have in their own directory, with precedence for the one who receives the new channel.
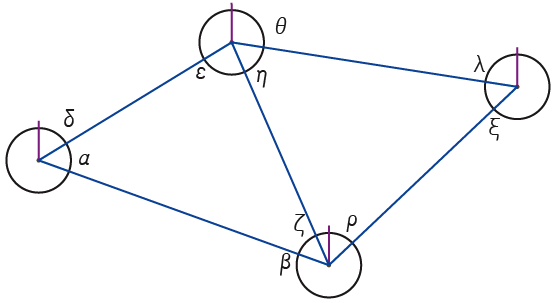
12) A fourth entity connects to the network. Remark that the denomination of entities (A, B, C, …) was necessary only for explanation and in fact these denominations are not necessary for entities because they denominate themselves with addresses defined in and by the network. Each entity has several addresses. Each one of them is available only for a single other entity. Remark also by the way that if the code was not angle ratio, the different addresses would perhaps be limited to the number of connexions of the most connected entity or to the maximal number of connexions defined beforehand by each entity. Each entity is, then, in contact with other entities who have different addresses for it. A priori, in a population, addresses can be repeated, but these identical addresses are not available for the same entities. We can see, at this stage, that an entity is connected to another one by a direct way or others indirect.
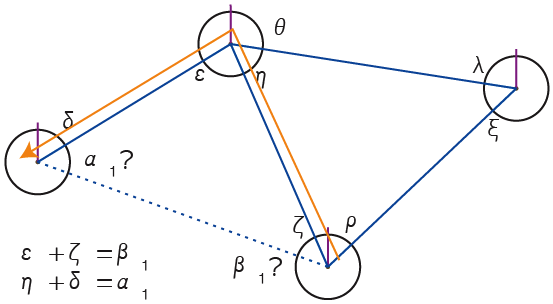
13) If a direct connexion between two entities is broken, entities don’t lose their respective addresses. They preserve a historic memory: at the time of connexion each entity has assigned an iteration to the address of the other entity (α1, α2, β1, …). Then, gradually, they can communicate again by the intermediary of other congeners: because their landmarks are angular, they search to find again the appropriate angular sum (here the address) of the lost congener, after which they recognize each other by dint of mutual memorization of their past link (at least their iterated addresses). They can even, each time there is a new connexion, calculate some indirect connexions (just in case…).
14) Here we are in a reticular and redundant self-eco-organized hierarchy. It’s no more necessary to have an external addressing and dedicated servers. The organization is distributed. It is neither centralized, nor multi-polar. We are strictly in anarchy.
Of course this scaffolding is conceptual: I have difficulty to see a spherical computer shaking arms in the space. Nevertheless, and here I leave to others either to forget me or to imagine the following, is it possible to install or act in a way that a such organization sets itself in place ?